为何 20 世纪初发现相对论和量子力学以后,近一百年现代物理再没有突破性的进展?
讲一讲近一百年现代物理的发展,讲一下这量子理论简史 :
「经过物理学家 100 多年的接力,人类终于了解了 4.9%的宇宙——量子理论简」史
从提出离散的光量子概念,到哥本哈根诠释对波函数与波粒二象性有更深入的理解;从整合物质波的波动力学与矩阵力学表述,到用场来统一描述电磁场与实物粒子;从统一电弱相互作用的杨-米尔斯理论,到描述强相互作用的量子色动力学;从简洁优雅的标准模型,到超越标准模型的弦理论以及其他理论。经过 100 多年的接力,物理学家逐渐建造起量子力学的宏伟殿堂,并颠覆了我们对世界的认知,然而,直到今天,这些理论只帮助人类理解了 4.9%的宇宙,剩下的更大部分的暗物质与暗能量我们仍然所知甚少。
「1 开宗立派:光量子,玻尔模型」
1900 年 12 月 14 日,精通音乐与作曲的德国物理学家普朗克(Max Planck,1858-1947)发现,若以一种量子化(quantization),即不连续、离散的观念来看待电磁波的能量随频率的分布,则可以得到关于黑体辐射(对于外来的电磁波无反射、无透射,完全吸收,这样的物体称为黑体(black body)。 黑体自身辐射出电磁波的现象称为黑体辐射。)的正确公式。尽管后来这一天被视为量子力学(或旧量子论)的诞生日,但当时普朗克本人对其中蕴含的革命性思想完全不以为意。
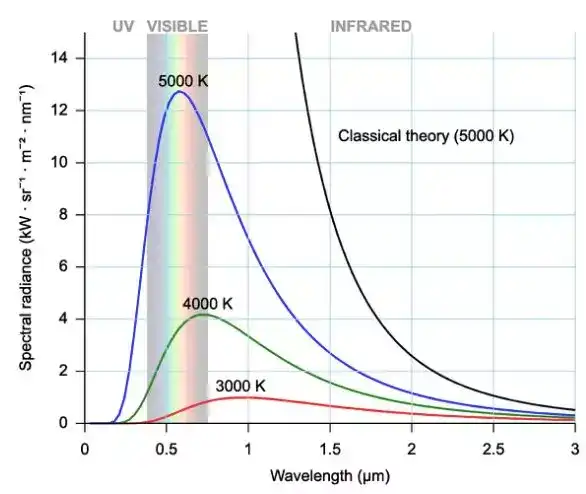
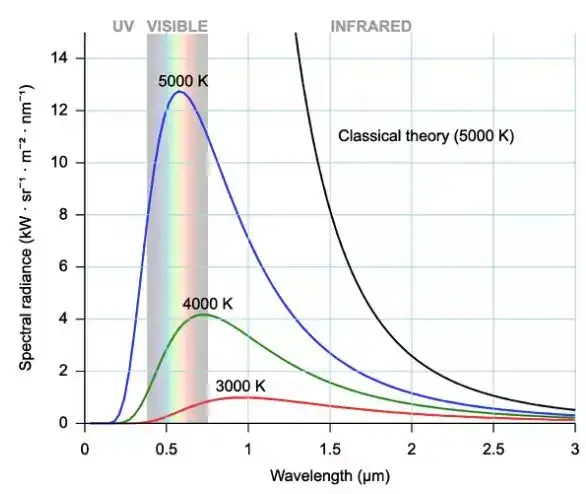
图 1:黑体辐射的频谱。 普朗克公式与实验结果完全一致。
1905 年,爱因斯坦(Albert Einstein,1879-1955)于苏黎世大学博士毕业,在这一年里,他连续发表了关于光电效应、布朗运动、狭义相对论以及质能关系的四篇论文,在物理学的四个不同领域中同时做出了开创性的巨大贡献。故 1905 年也被称为爱因斯坦奇迹年(Annus mirabilis)。其中,在对光电效应的研究中,爱因斯坦提出,量子化并不仅仅是一种数学上的技巧,光的能量本身就是量子化的。具体地说,对于频率为 ν 的光,其能量只能为
E = hν = ℏω (1)
的整数倍,其中 h = 6.626 × 10−34 J·s 被称为普朗克常数,ħ := h/2π 被称为约化普朗克常数;而一定频率下具有最小能量 (1) 的光被称为一个光量子(light quantum),或叫光子(photon);光的被发射或被吸收最少只能以一个光子的份额进行。当然,再考虑到由狭义相对论导出的光的能量动量关系 E = pc,我们还可获知,光的动量也是量子化的,即
p =h/λ 或 p = ℏk (2)
为一个光子所携带的动量。爱因斯坦的这种观点极具想象力与突破性,与人们长久以来存于脑中的关于物质世界的“连续性”这一既有观念形成了强烈的冲撞,以至于甚至遭到了作为量子论创始者的普朗克的反对。但它最终被实验证实,成为量子力学的肇始之一。
1913 年,为了解决原子光谱的离散性问题,以及在经典物理学框架下 卢瑟福原子模型(行星模型)的不稳定性,新婚第二年的玻尔(Niels Bohr,1885-1962)提出了关于原子结构的玻尔模型。其核心观点是,
• 电子稳定地位于原子核外一系列离散的能级上(即轨道能量与角动量 是量子化的);
• 只有当电子在两条能级间跃迁时,原子才以频率 ν = (∆E)/h 发射或吸收谱线。
对于氢原子等一些简单的情形,玻尔的理论给出了与实验结果〸分相符的说明。
以上这些工作构成了早期量子理论的主要部分。显然,它启发我们,微观世界应该有一个有异于经典物理学的全新的基础性规律。
「2 任督贯通:矩阵力学、波动力学、相对论量子力学」
在提出光量子概念以后的〸数年里,爱因斯坦进一步指出,波动性与量子性(粒子性)是光所必须具有的内在属性,这被称为光的波粒二象性。1924 年,在爱因斯坦光量子理论的启发下,大学早期曾就读于历史学专业的德布罗意(de Broglie,1892-1987)于其博士论文中提出,有必要把波粒二象性(wave-particle duality)拓展到全部微观粒子,即波可以具有量子(粒子)性,而普通实物粒子亦应可以具有波动性。由此,德布罗意给出物质波(matter wave)假设,它认为对于动量与能量分别为 p 与 E 的自由实物粒子,有如下波与其相联系:
λ = h/p, (3)
ν = E/h. (4)
德布罗意的物质波理论被他的导师转交爱因斯坦审阅,并得到了后者的大力赞赏,这不仅使他获得了博士学位,更将使整个量子理论进入一个新境界。


图 2:用电子作双缝实验,结果得到了如通常的波一般的干涉图样。从第一张图到第四张图,电子越来越多,干涉图样也越来越清晰。但值得注意,虽然图中每一个点表示有一个电子抵达探测屏,但点的离散状却并不意味着电子的“粒子性”。此实验由外村彰(Akira Tonomura)团队于 1988 年开展。
1925 年 6 月,刚在哥廷根大学获得教职的海森堡(Werner Heisenberg,1901-1976)因躲避过敏性鼻炎而前往德国北部的海姑兰岛。在那里,他一面品味着歌德的抒情诗集《西东诗集》(West-östlicher Divan),一面通过类比自傅立叶级数的方法,给出了描述量子理论的一个新方案,并找出了其中的关键:非对易性(noncommutativity)。在海森堡将他的结果寄给他大学时的老师玻恩(Max Born,1882-1970)后,后者意识到,海森堡的方法事实上就是将矩阵(matrix)的概念引了进来。在此基础上,当年内,他们就与玻恩的助教约尔旦(Pascual Jordan,1902-1980)一起,发展出了一套用系统化的矩阵语言来描述量子理论的新形式,称为矩阵力学(matrix mechanics)。
与此同时,正在剑桥攻读博士学位的狄拉克(Paul Dirac,1902-1984)指出,矩阵力学中的非对易性与分析力学中的泊松括号密切相关。在此基础上,狄拉克建立起了完整的正则量子化(canonical quantization)手续,并以此获得了博士学位。
在 1925 年受邀讲述德布罗意关于波粒二象性的论文后,时任苏黎世大学教授的薛定谔(Erwin Schrödinger,1887-1961)旋即于当年底到次年初建立了一个非相对论性的波动方程,即著名的薛定谔方程,并于 1926 年上半年完成了他所谓的波动力学的创建。因为 1920 年代物理学界对矩阵这一工具尚不熟悉,所以基于波函数(wave function)与偏微分运算的薛定谔方程甫一诞生,便受到了当时物理学家们的热烈赞赏。同年,在研究了 海森堡等人建立的矩阵力学之后,薛定谔证明了矩阵力学与波动力学的等价性。
至此,在以海森堡与薛定谔等人为主要代表的诸多物理学家的协同努力下,量子理论的内在逻辑与图景就得以清晰地展现在世人面前;早期量子理论(或叫旧量子理论)终于“跃迁”到了一个新的阶段,所谓现代量子力学宣告诞生。


图 3:薛定谔墓碑上镌刻着以他命字命名的方程。
薛定谔方程刚被提出之时,人们尚不清楚波函数的本质到底是什 么。 1926 年,玻恩提出了波函数的概率诠释 (玻恩定则),它宣称波函数是一种概率波幅,其模方代表粒子出现在某处的概率密度,且其在全空间的积分是归一化的。1927 年,在受聘于玻尔研究所与玻尔合作期间,海森堡提出了不确定性原理(uncertainty principle);而玻尔把波粒二象性与不确定性原理所反映的精神统归为互补原理(complementarity principle)。在这些观念的基础之上,以玻尔与海森堡等人为代表的物理学家对困扰人们已久的量子力学中的诸多新奇现象与问题,逐渐形成了一套自洽的看法,称为哥本哈根诠释 (Copenhagen interpretation)。 其主要包括:
• 体系的量子状态 (量子态)可以被波函数所完备地描述;
• 玻恩定则;
• 互补原理;
• 对应原理 (correspondence principle):大尺度系统的量子行为应可近似到经典状况;
• 测量导致波函数坍缩 (wave function collapse)。
一般而言,哥本哈根诠释已被当作量子力学的正统诠释而为人所接受。


图 4: 在 1947 年获得丹麦最高荣誉 Order of the Elephant 时,玻尔为自己设计的纹章。 其主体采用了中国传统的太极图;上方写有拉丁文 Contraria sunt Complementa,英译为 Opposites are Complementary, 汉译可为相反相成。
有趣的是,作为量子力学的重要创建人,爱因斯坦与薛定谔却都是哥本哈根诠释的坚定的反对者,或至少是执着的“挑刺”者。他们与哥本哈根学派之间产生了旷日持久的争论。其中,EPR 佯谬(EPR paradox)与薛定谔的猫(Schrödinger’s Cat)即他们于 1935 年分别提出的用以攻击后者的著名思想实验 (thought experiment)。不过,同样有趣的是,这两个诘难极大地推动了对量子力学中一些基本问题的研究与澄清,最后反倒被证明是哥本哈根诠释的有力论据。它们之中蕴含的量子纠缠(quantum entanglement)的现象,在今天已得到包括量子通信、量子计算等在内的越来越多的学科的应用。
不过,的确,以波函数坍缩为代表的量子力学中的一些本质问题,事实上仍未有得到完全的解决。诸多不同的诠释,如其中呼声最高的平行宇宙诠释,或叫多世界诠释(many-worlds interpretation)等,仍被人们为了最终解决这些问题而不断地研究着。


图 5:1927 年 10 月于比利时布鲁塞尔召开的第五次索尔维会议合影。 此次会议主题为“电子与光子”,是 专门为讨论新近建立的量子力学而举行的。
图 5:1927 年 10 月于比利时布鲁塞尔召开的第五次索尔维会议合影。 此次会议主题为“电子与光子”,是 专门为讨论新近建立的量子力学而举行的。虽然量子力学基本框架得到了广泛的认同,但就量子力学的诠释问题,会上的两位主角爱因斯坦与玻尔产生了激烈的交锋,这拉开了几乎持续了数〸年的所谓 “玻尔-爱因斯坦论战” 的序幕。图中几乎所有人都对量子力学或现代物理做出了重大贡献,下面列出他们每一个人的名字,以示崇高的敬意与铭记。每排皆按从左至右排。第 3 排:奥古斯特·皮卡尔德,亨里奥特,保罗·埃伦费斯特,爱德华·赫尔岑,西奥费·顿德尔,埃尔温·薛定谔,维夏菲尔特,沃尔夫冈·泡利,维尔纳·海森堡,拉尔夫·福勒,莱昂·布里渊;第 2 排:彼得·德拜,马丁·努森,威廉·劳伦斯·布拉格,亨德里克·克雷默,保罗·狄拉克,阿瑟·康普顿,路易·德布罗意,马克斯·玻恩,尼尔斯·玻尔;第 1 排:欧文·朗缪尔,马克斯·普朗克,玛丽·居里,亨德里克·洛伦兹,阿尔伯特·爱因斯坦,保罗·朗之万,查尔斯·古耶,查尔斯·威耳逊,欧文·理查森。
在对反常塞曼效应的研究中,泡利(Wolfgang Pauli,1900-1958)于 1924 年指出,电子应当有一个内禀量子数。在此基础上,次年他进一步提出了泡利不相容原理(Pauli exclusion principle);此原理宣称,不能有两个或更多个电子处于同样的量子态。1925 年 9 月,乌伦贝克(George Uhlenbeck,1900-1988)与古德斯米特(Samuel Goudsmit,1902-1978)指出,电子可以具有量值为 s = ℏ/2 的自旋(spin)角动量,此即为泡利所言之电子内禀量子数之来源。1927 年,泡利为自旋态与自旋算符分别引入了二分量旋量(spinor)波函数与 3 个二维表示矩阵,称为泡利矩阵,并将它们用在了薛定谔方程之中,从而得到了可以描述电子的非相对论性的运动方程,称为泡利方程。
至于泡利不相容原理,在泡利与狄拉克分别提出全同粒子(identical particles)这一概念后,可以简洁漂亮地发现,它是交换后使波函数反对称的粒子所必然遵循的。而至于为何交换后使其波函数反对称的粒子偏偏是具有半整数自旋的粒子(称为费米子),这个问题则要等到量子场论中应用狭义相对论的因果律才能得以说明。
自从爱因斯坦于 1905 年提出狭义相对论以后,人们自然有理由相信,任何一个高能理论都应当具有相对论协变性。1926 年,克莱因(Oskar Klein,1894-1977)与戈登(Walter Gordon,1893-1939)提出了最简单的相对论性波动方程,称为克莱因-戈登方程。但因其面临负能量与负概率的困难,而且也不能正确解释氢原子中的问题,自提出以后的很长一段时间内,它的真正含义并未能为物理学家所领会。
面对泡利方程与克莱因-戈登方程各自存在的问题,狄拉克于 1928 年建立起了一个能避免负概率的相对论性方程,即狄拉克方程。此方程强大 的解释力旋即得到了展现,而且其内在地包含了电子的自旋,〸分优美。 于是,狄拉克方程自然成了相对论量子力学(Relativistic Quantum Mechanics)的基本方程。但是,狄拉克方程身上仍然存在着负能量问题。为此,1929 年到 1931 年,狄拉克通过所谓狄拉克海(Dirac Sea)的手段预言了正电子(positron)的存在(并于次年得到证实),从而使反物质(antimatter)这一概念第一次进入了人类思维。
1930 年,在他划时代的集大成之作《量子力学原理》(The Principles of Quantum Mechanics)里,狄拉克指出
• 量子态是希尔伯特 空间中的矢量;
• 可观测量(observables)即作用在希尔伯特 空间上的自伴算子 (厄米矩阵,Hermitian matrix)。
以此,狄拉克将海森堡的矩阵力学与薛定谔的波动力学整合到了同一个数学形式之中。同期, 冯·诺伊曼(John von Neumann,1903-1957)亦给出了相似的工作,这反映在他出版于 1932 年的《量子力学的数学基础》(Mathematical Foundations of QuantumMechanics)一书中。狄拉克与冯·诺伊曼的工作,共同形成了所谓狄拉克-冯·诺伊曼公理。连同哥本哈根诠释一起,我们也可将之视为量子力学的公设(postulates of quantum mechanics)。
至此,量子力学这座巍巍大厦,就严格地确立了。
「3 登峰造极:量子场论,粒子物理标准模型」
1925 年到 1926 年间,玻恩、海森堡与约尔旦把电磁场看成是无穷维谐振子(harmonic oscillator),进而通过正则量子化的方法给出了电磁场的量子化。但他们的工作中并没有把相互作用考虑进来。1927 年,史上首次,狄拉克作了有关于电磁相互作用的量子力学计算,并提出了量子电动力学(QED: quantum electrodynamics)一词。 在此工作中,为将电磁场进行量子化,狄拉克天才地创造了产生湮灭算符(Creation and annihilation operators)的办法。
1928 年到 1934 年这一时期,约尔旦、维格纳(Eugene Wigner,1902-1995)、海森堡、泡利与费米(Enrico Fermi,1901-1954)通过反对易(anticommutativity)的手段——即现在所谓的费米子的约尔旦-维格纳量子化——表明,正像量子化以后电磁场的激发态对应不同数目的光子一样,作为一种实物粒子,电子亦可被视为某种相应的场量子化以后的激发元。这样,借助于量子作为桥梁,电磁场与实粒物子就都统一到了场(field)这一概念之下。最终,1934 年,海森堡将狄拉克方程,以及先前的克莱因-戈登方程,重新阐释为描述不同粒子的场的运动方程,而非单粒子波函数的运动方程。在这种图景之下,方程解的所谓负能量问题迎刃而解:它本身就描述了反物质,而完全不须引入狄拉克海这一概念。
1930 年以及之后,奥本海默(Julius Oppenheimer,1904-1967)等人指出,在微扰计算中,量子电动力学的高阶项会现一些不可避免的无穷大,理论发散。 量子场论由此进入第一次低潮。
时间转眼来到了二战后期。在贝特(Hans Bethe,1906-2005)1947 年工作的启发下,施温格(Julian Schwinger,1918-1994)、费曼(Richard Feynman,1918-1988)、朝永振一郎(Tomonaga,1906-1979)与戴森(Freeman Dyson,1923-)等人于 1950 年前后建立起了一套系统化地消除量子电动力学中高阶发散的手续,称为重整化 (renormalization)(事实上, Ernst Stueckelberg(斯蒂克尔堡, 瑞士, 1905-1984) 已于 1943 年独立地建立起了重整化的工作,但未能引起当时物理学界的重视。)。在施以重整化后,QED 对电子的反常磁矩、氢原子光谱的精细结构(兰姆移位,Lamb Shift)等作出的计算与实验结果的吻合度之高达到了非凡的地步,以至于赢得了 “the jewel of physics” 的美誉。
在建立重整化的过程中,费曼发明了表征各阶展开项的图形化技术,称为费曼图(Feynman diagram)。如今,费曼图已作为一种形象化的物理直觉,深刻融入了理论物理学家的思维之中。与此同时,费曼还给出了量子力学的又一种实现方案:路径积分表述(path integral formulation)。此理论并不预先要求量子体系必须满足经典的最小作用量原理(least action principle),而最终却可以得出与后者相同的结果。 路径积分的出现,使人们对量子力学本质的理解得到了进一步加深。

图 6:关于路径积分的一个诙谐但正确的图片。
随着量子电动力学中重整化的胜利,人们很乐观地相信,量子场论这种思想很快就可以为所有微观现象提供一个完整的描述框架。然而,随后人们发现,1)当时描述弱相互作用的费米理论是不可重整化的,2)强相互作用中耦合常数较大(∼1),无法做微扰展开;这些与量子场论的基本精神恰是严重相违背的。于是,量子场论进入了长达〸数年的第二次艰难探索期。
转机始于来自中国的两个年轻人。1954 年,杨振宁(1922-)与米尔斯(Robert Mills,1927-1999)把定域规范变换(local gauge transformation)由量子电动力学的 U(1)阿贝尔情形,推广到了更高维的非阿贝尔情形,从而建立了非阿贝尔规范理论,又称为杨-米尔斯(Yang-Mills)理论。日后的发展将表明,
• 规范不变性(gauge invariance)是所有相互作用所皆须遵循的一般原理,而
• 杨-米尔斯理论是它们的共同的表述框架。
1956 年,李政道(1926-)与杨振宁共同指出了弱相互作用下宇称不守恒(parity violation),这直接为电磁相互作用与弱相互作用的统一指出了正确方向。
在以上工作的基础上,1960 年与 1964 年,格拉肖(Sheldon Glashow,1932-)与萨拉姆(Abdus Salam,1926-1996)分别独立建立了统一电磁相互作用与弱相互作用的理论。1964 年,在南部阳一郎(Yoichiro Nambu,1921-2015)关于自发对称破缺(spontaneous symmetry breaking)工作的基础上,希格斯(Peter Higgs,1929-)等人指出,自发对称破缺可以使杨-米尔斯理论中的中间玻色子(规范场)获得质量。该理论日后被称为希格斯机制。1967 年,温伯格(Steven Weinberg,1933-)与萨拉姆把希格斯机制引入电弱理论,从而成功使电弱相互作用中规范玻色子获得质量。1971 年,特·胡夫(Gerard ’t Hooft,1946-)与他的导师韦尔特曼(Martinus Veltman,1931- )证明了杨-米尔斯 理论的可重整化性。 至此,电弱统一理论(又称为 GSW 模型)最终得到完全确立。1973 年,由其预言的中性流被实验发现以后,GSW 模型得到了广泛的接受。
1964 年,在对纷繁复杂的强子的研究中,盖尔曼(Murray Gell-Mann,1929-)与茨威格(George Zweig,1937-)分别独立地提出了夸克(quarks)理论。1968 年,斯坦福线性加速中心(SLAC)在实验中确认了上夸克与下夸克的存在。1972 年,弗里奇(Harald Fritzsch ,1943-)与盖尔曼等人在杨-米尔斯规范理论的基础上建立了描述强相互作用的量子色动力学(QCD: quantum chromodynamics)。1973 年,格娄斯(David Gross,1941-)、维尔切克(Frank Wilczek,1951-)以及波利策(Hugh Politzer,1949-)发现了强相互作用的渐进自由(Asymptotic freedom),即重整化后,随着能量尺度增加,强相互作用耦合常数变小的现象。这就使得微扰展开在 QCD 中的进行成为了可能。
至此,人类目前所知的自然界四种基本相互作用中,除了万有引力,其余三种皆得到了以杨-米尔斯规范理论为基础的理论 QED、GSW 理论、QCD——此即量子场论(QFT: quantum field theory)的主要组成部分——的完备的描述。量子场论对此三种基本相互作用的这种解释图景,称为粒子物理的标准模型 (standard model)。
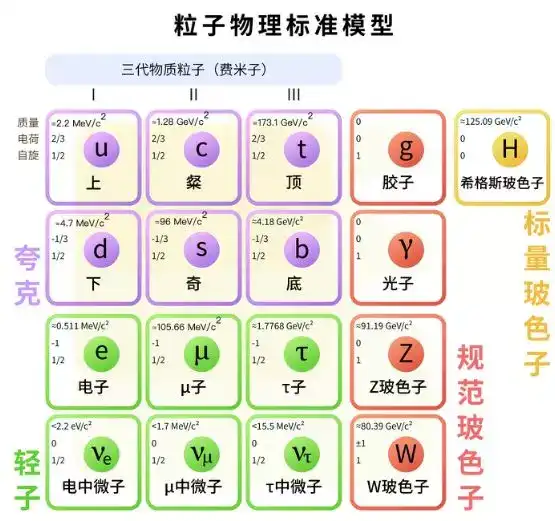

图 7:标准模型中的基本粒子及其分类。基本粒子共有 62 个,计算如下。夸克:6 个 ×3 色 ×2(正反粒 子)= 36;轻子:6 个 ×2(正反粒子)= 12; 规范玻色子: 8 胶子 +1 光子 +1 Z 玻色子 +2 W 玻色子 =13;希格斯子:1。
「4 谁与争锋:超越标准模型」
尽管取得了卓越的成功,标准模型亦留下了不少未能回答的问题,如质量形成机制、强 CP 问题、中微子振荡等等。另外,建立在广义相对论基础上的宇宙学标准模型 (ΛCDM 模型),亦给我们提出了几个亟待解决的重大疑问,如重子不对称、暗物质(dark matter)、暗能量(dark energy)等。通过威尔金森微波各向异性探测器(WMAP)耗时七年的观测,人们得出,在宇宙物质总量中,为粒子物理标准模型所描述的常规物质只占 4.9%,而暗物质占到了 26.8%,暗能量的份额更是高达 68.3%。
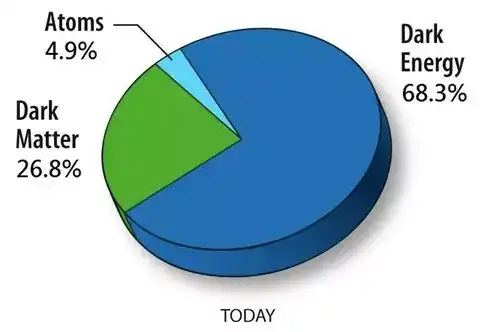

图 8:宇宙中的暗能量与暗物质远远多于常规物质。
我们期待着理论物理学能对这些问题继续给出合理的回答,于是这就产生了所谓超越标准模型的物理学(BSM: physics beyond standard model)。对此,目前的主流方案是引入超对称(SUSY: supersymmery)。 引入超对称的标准模型,又叫超杨-米尔斯(SYM)理论。随着标准模型最后一块拼图希格斯玻色子于 2012 年在 LHC 上被发现,人类的下一个目标就是发现超对称粒子。我国目前正在推动建设的环形正负电子对撞机(CEPC)如果能够实现这一愿景,那将为理论物理学甚至整个人类科学带来极大的突破。
以上所说的诸多问题,属于更广一类的尚未解决的物理学问题 (usoloved problems inphysics)。要解决他们,事实上已涉及到了广义相对论与量子理论的统一,即量子引力(quantum gravity)这个课题。 目前,我们相信,诞生于 1970 年代的超弦理论 (superstring theory)是这一任务的最有前景的候选者之一。



评论区